If you have data such as velocity and time traveled, would you be able to calculate the total distance journeyed? Let’s discover how to tackle this question with spreadsheets! We’ll first begin by calculating distance traveled when velocity is constant. Then we’ll approach a more realistic situation of varying velocity using the Mid Rectangular Approximation Method (MRAM)!
Constant Velocity
Let’s imagine you drive a car that operates under only one speed (30 miles per hour), and you drive the car for exactly 1 hour. How far would you have gone? Exactly 30 miles! After two hours, you would have covered a total distance of 60 miles! (or 30 miles/hr x 2 hrs)
To calculate the distance traveled when the speed or velocity is constant, multiply the velocity and the time elapsed, as shown in the equation below:
Distance (D) = Velocity (V) x Time (T)
Keep in mind that if the unit for Time (T) is inconsistent with that of Velocity (V), first convert the units. For instance, let’s imagine the total travel time is 30 minutes, and my velocity is 30 miles/hour. To calculate the distance traveled, first convert the units of Time from minutes to hours and then multiply the velocity. So, 30 mins x (1 hr / 60 mins) = 1 /2 hrs x 30 miles/hr = 15 miles!
But what if Velocity is not constant?
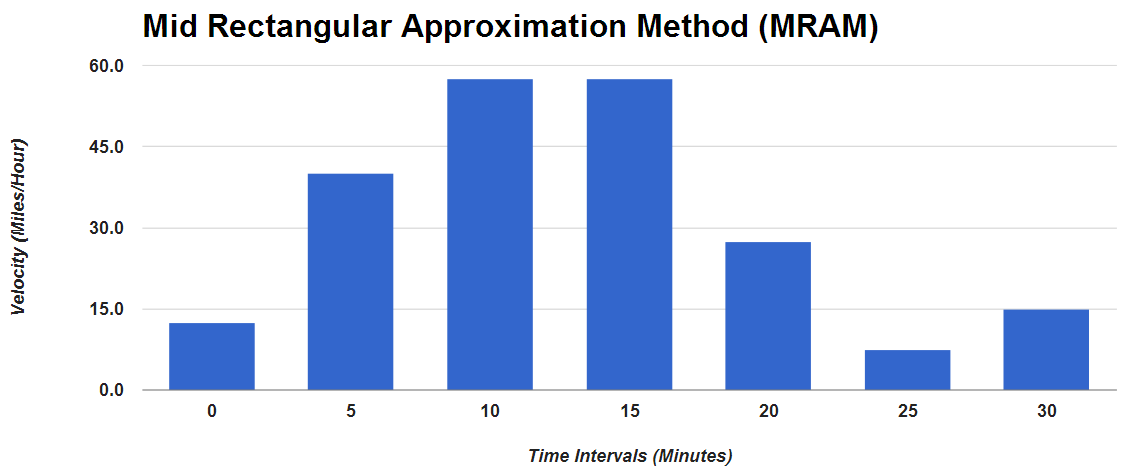
When velocity is not constant, how can we approach this problem? Let’s approach this with the Mid Rectangular Approximation Method (MRAM) to answer the question: What distance did I travel in my 30 minute commute from home to the office?
Using a spreadsheet, we note our velocity at five minute intervals as shown to the right. At time zero, my speed is zero. At five minutes, I check my velocity, which registers at 25 miles/hr. At the 25 minute interval, I was at a stop sign, so my velocity was zero. I continue until I reach the 30 minute interval.
To calculate the distance using MRAM, we calculate the average of the two points of each interval. We then sum up these averages and multiply by 5 / 60. Why 5 / 60? The numerator indicates the 5 minute intervals. Given the velocities are in miles per hour, we convert the interval units from minutes to hours by multiplying a factor of 1 / 60. Based on our velocities, the approximate distance traveled is 18.125 miles!
In the graph, the y-axis is velocity, and the x-axis is the time interval. The distance traveled is the sum of the rectangular areas with each rectangular height being the midpoint or average velocity of 2 interval points.
Now if we were to measure the velocities are smaller intervals – say 2.5 minutes instead of 5 minutes, the rectangles become closer together, improving the accuracy of the estimated distance traveled!
Give it try!
Track your velocity every 2.5 minutes and use MRAM to estimate your distance traveled. The related spreadsheet, shown below, can be found here: How to Measure Distance Traveled. To edit it, first create a copy of it on your Google drive.
[googleapps domain=”docs” dir=”spreadsheet/pub” query=”key=0ArU-OSCYb_YpdGE1Y2lJdEVRdWNYdDVlUXM3ekQxemc&output=html&widget=true” width=”640″ height=”300″ /]