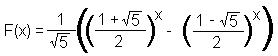What do sunflowers, shells, honeybees, the Parthenon, and human arm length measurements have in common? All reflect a remarkable pattern of numbers. Now just where does this intriguing sequence of numbers come about? Let’s discover the Fibonacci sequence and the Golden Ratio and how we can use spreadsheets to calculate them!
The Rabbit Problem
The origin of the Fibonacci sequence can be traced to a thought experiment about rabbits in the 13th century. Leonardo Pisano Fibonacci posed this question: In an ideal world, how many pairs of rabbits can be produced from a single pair of rabbits in one year?
Let’s assume that rabbits reproduce after they are at least 1 month old and females always produce one pair of rabbits – a male and a female. So, at the end of the first month, we have one pair of rabbits, who are now 1 month old. By the end of the second month, the female gives birth to a pair of newborns, which results in a total of 2 pairs of rabbit. Another a third month passes, the original pair of rabbits produce a pair, and the previous offspring grows to adulthood, leaving a total of 3 pairs.
As this continues on and on for each month, the number of pairs is 1, 1, 2, 3, 5, 8….If we look carefully, we find a pattern with this sequence in numbers: each number is a sum of the previous two!
How to Calculate the Fibonacci series:
So, the 1st Fibonacci term is 1, the 2nd is 1, the 3rd is 2, the 4th is 3, and so on. But what if wanted to find we find say the 50th Fibonacci term? Computationally, this could be a bit more challenging.
Happily, we can easily set up a formula that takes the sum of the previous two numbers in a spreadsheet! We can set this formula in cell C5 (shown in Cell D5) and then simply copy and paste it down. By the end of 1 year or 12 month, we find that the total number of pairs is 233! If curious about the rest of the numbers in the series, we can very simply copy and paste the formula downwards until we reach the 50th term. As seen in the spreadsheet, we find that the 50th Fibonacci term is a staggering 12,586,269,025!
[googleapps domain=”docs” dir=”spreadsheet/pub” query=”key=0ArU-OSCYb_YpdF9pa2dxNG5BaHFWRkhpMlZoaVJ4LVE&output=html&widget=true” width=”600″ height=”384″ /]
Another way to calculate the Fibonacci series would be to use Binet’s formula. In 1843, Jacques Binet discovered a formula that can also compute the nth term of the Fibonacci series, as shown below.
And yes – there is still another way to calculate the nth term of the Fibonacci series, which involves using summation notation, binomial theory, and Pascal’s triangle. For those interested in how we can set up Pascal’s triangle in a spreadsheet, please see John Baker’s article “Pascal Pyramids: a mathematical exploration using spreadsheets” in Spreadsheets in Education (eJSiE)*
Golden Ratio
Also known as the Golden Mean, the Golden Ratio is the ratio between the numbers of the Fibonacci numbers. In a spreadsheet, we can divide the Fibonacci numbers and as we do so, we can see the Golden Mean becomes approximately 1.618. If you divide the number of female honeybees by the male honeybees in any given hive, the resulting number is 1.618. Measure the length of your shoulder to fingertips and divide that by the length of you elbow to fingertips. Again – what you do find? The intriguing Golden Mean!
*Resources: